Стандартный вид числа. Стандартная, она же научная форма записи числа. Порядок величины. Разница на порядок. Зачем это придумали.

Стандартный вид числа. Стандартная, она же научная форма записи числа. Порядок величины. Разница на порядок. Зачем это придумали.

Любое рациональное число может быть представлено в виде:

Стандартная, она же научная форма записи числа. Порядок величины. Разница на порядок.

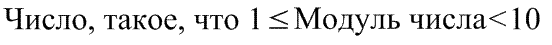	умножить на
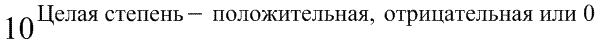Эта часть записи называется Мантиссой числа в стандартной (научной) форме.		А эта часть называется Порядком числа в стандартной (научной) форме.

• Пример 1: Число 7984 в стандартной форме записывается как 7,984*10³ , где 7,984 - мантисса а 10³ - порядок.
• Пример 2 : Величины 890 и 45932, записанные в стандартной форме выглядят как: 8,9*10² и 4,5932*10⁴ и отличаются на 2 порядка = имеют разницу в 2 порядка. Числа 7,5 и 75 различаются на порядок ( на 1 порядок) = имеют разницу в 1 порядок, что бы там в телевизоре не думали. И так далее...

• Очевидно, что при сложении и вычитании чисел записанных в стандартной форме и имеющих один порядок, достаточно сложить или вычесть мантиссы.
  • Пример 3: 7,2*10³⁴ + 1,2*10³⁴= (7,2+ 1,2)*10³⁴=8,4*10³⁴

• Единственный способ корректно сложить или вычесть числа разных порядков - это выразить одно из них в нестандартной форме:
  • Пример 4: 9,9*10¹³ + 9,9*10¹²=9,9*10¹³ + 0,99*10¹³= (9,9+ 0,99)*10¹³=10,89*10¹³=1,089*10¹⁴

• Очень удобно проводить операции умножения и деления с числами, записанными в стандартной форме, пользуясь правилами действий со степенями:
  • Пример 5: 4,0*10³x 2,25*10²=(4,0x2,25)x(10³⁺²)= 9,0*10⁵
  • Пример 6: 5,0*10⁶ /2,5*10³=(5,0/2,5)x(10^6-3)= 2,0*10³

И теперь, если уж Вы дочитали до этого места, самое главное - зачем это придумано: попробуйте сравнить на глаз числа 970984567234109879 и 1211121111211121112125? Впечатляет? А попробуйте их же в стандартном виде: 9,70984567234109879*10¹⁷ и 1,211121111211121112125*10²¹. Понятно, что первое на 4 порядка меньше? Понятно, что величина первого по отношению ко второму ниже, чем точность большинства расчетных моделей? Понятно, что в большинстве практических случаев первую величину вообще не следует брать в расчет, если вклад величин в процесс пропорционален? Понятно, что изменение второй величины на 10% значительно превосходит изменение первой в 3 раза? и т.д. Просто, оказывается, инженеры их жены и дети так устроены, что с этими числами очень удобно работать.