Второй закон термодинамики. Энтропия. Определение энтропии. Эффективность теплового двигателя. Тепловой цикл Карно. Неубывание энтропии

2-й закон термодинамики. Энтропия. Определение энтропии. Эффективность теплового двигателя. Тепловой цикл Карно. Неубывание энтропии.     Вариант для печати.

Второй закон связан с понятием энтропии, являющейся мерой хаоса (или мерой порядка). Второй закон термодинамики гласит, что для вселенной в целом энтропия возрастает.

Существует два классических определения второго закона термодинамики :

1. Кельвина и Планка: Не существует циклического процесса, который извлекает количество теплоты из резервуара при определенной температуре и полностью превращает эту теплоту в работу. (Невозможно построить периодически действующую машину, которая не производит ничего другого, кроме поднятия груза и охлаждения резервуара теплоты)
2. Клаузиуса: Не существует процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому. (Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара)

Оба определения второго закона термодинамики опираются на первый закон термодинамики, утверждающий, что энергия убывает. Второй закон связан с понятием энтропии (S).

Энтропия порождается всеми процессами, она связана с потерей системы способности совершать работу. Рост энтропии - стихийный процесс. Если объем и энергия системы постоянны, то любое измение в системе увеличивает энтропию. Если же объем или энергия системы меняются, энтропия системы уменьшается. Однако, энтропия вселенной при этом не уменьшается.

Для того, чтобы энергию можно было использовать, в системе должны быть области с высоким и низким уровнями энергии. Полезная работа производится в результате передачи энергии от области с высоким уровнем энергии к области с низким уровнем энергии.

• 100% энергии не может быть преобразовано в работу
• Энтропия может вырабатываться, но не может быть уничтожена

Эффективность теплового двигателя

Эффективность теплового двигателя, действующего между двумя энергетическими уровнями , определена в пересчете на абсолютные температуры

• η = ( T_h - T_c ) / T_h = 1 - T_c / T_h
  • где
  • η = эффективность
  • T_h = верхняя граница температуры (K)
  • T_c = нижняя граница температуры (K)

Для того, чтобы достичь максимальной эффективности T_c должна быть на столько низкой, на сколько это возможно. Чтобы эффект был 100% -м, T_c должна равнятся 0 по шкале Kельвина. Практически это невозможно, поэтому эффективность всегда меньше 1 (менее 100%).

• Изменение энтропии > 0 Необратимый процесс
• Изменение энтропии= 0 Двусторонний процесс (обратимый)
• Изменение энтропии < 0 Невозможный процесс (неосуществимый)

Энтропия определяет относительную способность одной системы влиять на другую. Когда энергия двигается к нижнему энергетическому уровню, где уменьшается возможность влияния на окружающую среду, энтропия увеличивается.

Определение энтропии

Энтропия в системе постоянного объема определяется как :

• dS = dH / T
  • где
  • S = энтропия (кДж/кг*К)
  • H = энтальпия (кДж/кг) (иногда вместо dH записывают dQ = количество теплоты, сообщенное системе )
  • T = абсолютная температура (K - градусы Кельвина) 

Изменение энтропии системы вызвано изменением содержания тепла в ней. Изменение энтропии равно изменению тепла системы деленной на среднюю абсолютную температуру ( T_a):

Тепловой цикл Карно. Цикл Карно— идеальный термодинамический цикл.

dS = dH / T_a  Сумма значений (dH / T) для каждого полного цикла Карно равна 0. Это происходит из-за того, что каждому положительному H противостоит отрицательное значение H.

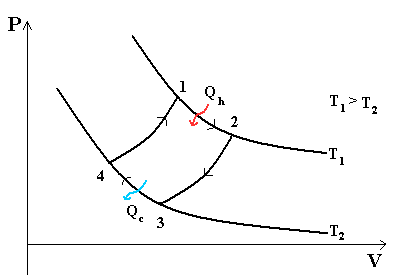
В тепловом двигателе, газ (реверсивно) нагревается (reversibly heated), а затем охлаждается. Модель цика следующая: Положение 1 --( изотермическое расширение) --> Положение 2 --( адиабатическое расширение) --> Положение 3 --(изотермическое сжатие) --> Положение 4 --(адиабатическое сжатие) --> Положение 1

• Положение 1 - Положение 2: Изотермическое расширение
  • Изотермическое расширение. В начале процесса рабочее тело имеет температуру T_h , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты Q_H. При этом объём рабочего тела увеличивается. Q_H=∫Tds=T_h (S₂-S₁) =T_h ΔS
• Положение 2 - Положение 3: Адиабатическое расширение
  • Адиабатическое (изоэнтропическое) расширение. Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
• Положение 3 - Положение 4: Изотермическое сжатие
  • Изотермическое сжатие. Рабочее тело, имеющее к тому времени температуру T_c, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты Q_c. Q_c=T_c(S₂-S₁)=T_c ΔS
• Положение 4 - Положение 1: Адиабатическое сжатие
  • Адиабатическое (изоэнтропическое) сжатие. Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия. Поэтому цикл Карно удобно представить в координатах T и S (температура и энтропия). Законы термодинамики были определены эмперическим путем (эксперементально). Второй закон термодинамики - это обощение экспериментов, связанных с энтропией. Известно, что dS системы плюс dS окружающей среды равно или больше 0 - закон неубывания энтропии. Энтропия адиабатически изолированной системы не меняется!

Пример - Энтропия при нагревании воды

• Процесс нагревания 1 кг воды от при нормальных условиях.C (273 до 373 K)^o0 до 100
  • C = 0 кДж/кг (удельная - на единицу массы)^o при 0 см. удельная энтальпия для воды
  • Удельная энтальпия для воды при 100^oC = 419 кДж/кг
    • Изменение удельной энтропии :
    • dS = dH / T_a  = ((419 кДж/кг) - (0 кДж/кг)) / ((273 К + 373 К)/2) = 1.297 кДж/кг*К

Пример - Энтропия при испарении воды

• Процесс превращения 1 кг воды при 100^oC (373 K) в насыщенный пар при 100^oC (373 K) при нормальных условиях.
  • Удельная энтальпия пара при 100^oC (373 K) до испарения = 0 кДж/кг
  • Удельная теплота парообразования 100^oC (373 K) при испарении = 2 258 кДж/кг
    • Изменение удельной энтропии:
    • dS = dH / T_a   = (2 258 - 0) / ((373 + 373)/2)  = 6.054 кДж/кг*К

Полное изменение удельной энтропии испарения воды - это сумма удельной энтропии воды (при 0^oC) плюс удельная энтропия пара (при температуре 100^oC).