Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида. Вариант для печати.
Графики тригонометрических функций.
Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд - углы в радианах.
Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0o до 360o, показаны на рисунках ниже.
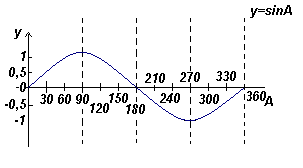
График функции y=sinA (синусоида) |
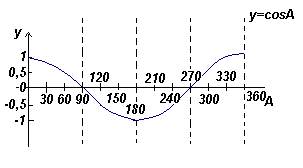
График функции y=cosA (косинусоида) |
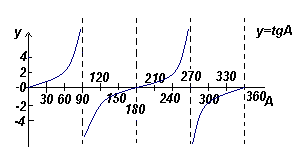
График функции y=tgA (тангенсоида) |
|
Из графиков видно что:
- Графики синуса и косинуса колеблются в пределах между -1 и 1
- Кривая косинуса имеет ту же форму, что и кривая синуса, но сдвинута относительно нее на 90o
- Кривые синуса и косинуса непрерывны и повторяются с периодом 360o , кривая тангенса имеет разрывы и повторяется с периодом 180o .
Углы произвольной величины
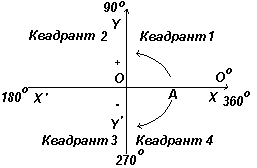 На рис. слева показаны перпендикулярные оси ХХ' и YY'; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О - отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке - отрицательным. На рис. слева показаны перпендикулярные оси ХХ' и YY'; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О - отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке - отрицательным.
График. Положительное или отрицательное направление при движении по окружности.
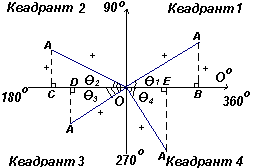 Пусть ОА вращается против часовой стрелки таким образом, что Θ1 - любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.) Пусть ОА вращается против часовой стрелки таким образом, что Θ1 - любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.)
Пусть ОА вращается дальше таким образом, что Θ2 - любой угол во втором квадранте, и построим АС так, чтобы образовался прямоугольный треугольник ОАС. Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 - любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ .
График. Поcтроение углов в различных квадрантах.
 Пусть ОА вращается дальше таким образом, что Θ4- любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ4= -/+= -; cos Θ4=+/+=+; tg Θ4= -/+= -. Пусть ОА вращается дальше таким образом, что Θ4- любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ4= -/+= -; cos Θ4=+/+=+; tg Θ4= -/+= -.
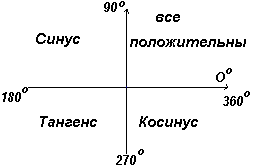
В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем - только тангенс, в четвертом только косинус, что и показано на рис. слева.
График. Положительные и отрицательные значения синусов, косинусов и тангенсов.
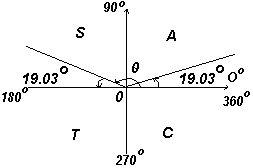
Знание углов произвольной величины необходимо при нахождении, например, всех углов между 0o и 360o , синус которых равен, скажем, 0,3261. Если ввести в калькулятор 0,3261 и нажать кнопку sin-1, получим ответ 19,03o . Однако существует второй угол между 0o и 360o , который калькулятор не покажет. Синус также положителен во втором квадранте. Другой угол показан на рис. ниже как угол Θ, где Θ=180o - 19,03o = 160,97o . Таким образом, 19,03o и 160,97o - это углы в диапазоне от 0o до 360o , синус которых равен 0,3261.
Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины.
График. Нахождение всех углов по заданному значению синуса (пример)
Пример 1
Найти все углы в диапазоне от 0o до 360o , синус которых равен -0,7071
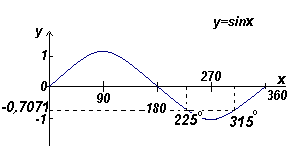
Решение:
Углы, синус которых равен -0,7071o находятся в третьем и четвертом квадранте, поскольку синус отрицателен в этих квадрантах (смотри рис. слева).
График. Нахождение всех углов по заданному значению синуса (пример)
Из следующего рисунка Θ = arcsin 0,7071 = 45o. Два угла в диапазоне от 0o до 360o, синус которых равен -0,7071, это 180o +45o =225o и 360o - 45 o = 315o .
.gif)
Примечание. Калькулятор дает только один ответ.
График. Нахождение всех углов по заданному значению синуса (пример)
Пример 2
Найти все углы между 0o и 360o , тангенс которых равен 1, 327.
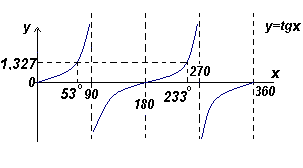
Решение:
Тангенс положителен в первом и третьем квадрантах - рис. слева.
График. Нахождение всех углов по заданному значению тангенса (пример)
Из рис ниже Θ = arctg1,327= 53o . .gif)
Два угла в диапазоне от 0o до 360o , тангенс которых равен 1,327, это 53o и 180o + 53 o, т.е. 233o .
График. Нахождение всех углов по заданному значению тангенса (пример)
Построение синусоиды и косинусоиды
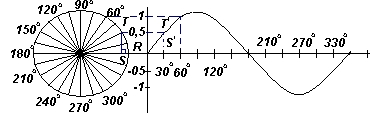 Пусть ОR на рис. слева- это вектор единичной длины, свободно вращающийся против часовой стрелки вокруг О. За один оборот получается круг, показанный на рис. и разделенный секторами по 15 o. Каждый радиус имеет горизонтальную и вертикальную составляющую. Например, для 30o вертикальная составляющая - это ТS, а горизонтальная - ОS. Пусть ОR на рис. слева- это вектор единичной длины, свободно вращающийся против часовой стрелки вокруг О. За один оборот получается круг, показанный на рис. и разделенный секторами по 15 o. Каждый радиус имеет горизонтальную и вертикальную составляющую. Например, для 30o вертикальная составляющая - это ТS, а горизонтальная - ОS.
График. Построение синусоиды.
Из определения тригонометрических функций
sin30o=TS/TO=TS/1, т.е. TS= sin30o и cos30o=OS/TO=OS/1, т.e. OS=cos30o
Вертикальную составляющую TS можно перенести на график в виде T'S', что равно значению, соответствующему углу 30o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.
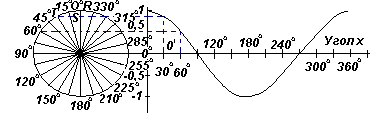
Если все горизонтальные составляющие, подобные OS, спроецировать на график зависимости у от угла х, получится косинусоида. Эти проекции легко визуализировать, перерисовывая круг с радиусом OR и началом отсчета углов от вертикали, как показано на рисунке слева.
Из рис. слева видно, что синусоида имеет ту же форму, что и косинусоида, но смещенная на 90o.
График. Построение косинусоиды.
Синусоидальные и косинусоидальные графики
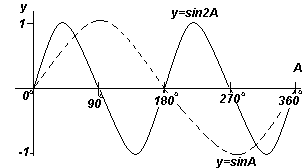
График. y=sinA и y=sin2A (синусоиды). |
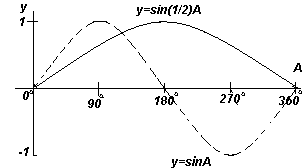
График. y=sinA и y=sin(1/2)A (синусоиды). |
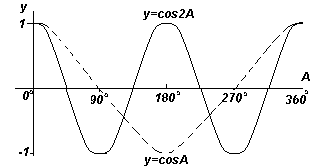
График. y=cosA и y=cos2A (косинусоиды). |
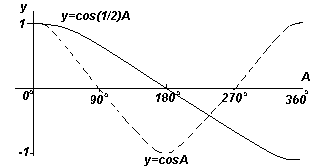
График. y=cosA и y=cos(1/2)A (косинусоиды). |
Периодические функции и период
Каждый из графиков функций, показанных на четырех рис. выше, повторяется при увеличении угла А, поэтому их называют периодическими функциями.
Функции y=sinA и y=cosA повторяются через каждые 360o (или 2π радиан), поэтому 360o называется периодом этих функций. Функции y=sin2A и y=cos2A повторяются через каждые 180o (или π радиан),поэтому 180o - это период для данных функций.
В общем случае если y=sinpA и y=cospA (где р - константа), то период функции равен 360o/p (или 2π/p радиан ). Следовательно, если y=sin3A, то период этой функции равен 360o/3= 120o, если y=cos4A, то период этой функции равен 360o/4= 90o.
Амплитуда
Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1). Однако, если y=4sinA, каждая из величин sinA умножается на 4, таким образом, максимальная величина амплитуды - 4. Аналогично для y=5cos2A амплитуда равна 5, а период - 360o/2= 180o.
Пример 3.
Построить y=3sin2A в диапазоне от А= 0o до А=360o. 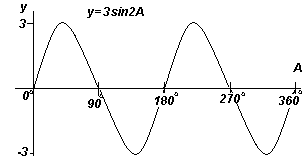
Решение:
Амплитуда =3, период = 360o/2 =180o.
График. Построение y=3sin2A (синусоида).
Пример 4.
Построить график y=4cos2x в диапазоне от х=0o до х=360o 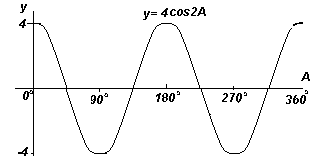
Решение:
Амплитуда = 4. период = 360o/2 =180o.
График. Построение y=4cos2x (косинусоида).
Углы запаздывания и опережения
Кривые синуса и косинуса не всегда начинаются в 0o . Чтобы учесть это обстоятельство, периодическая функция представляется в виде y=sin(A± α), где α - сдвиг фазы относительно y=sinA и y=cosA.
.gif) Составив таблицу значений, можно построить график функции y=sin(A-60o), показанный на рис. слева. Если кривая y=sinA начинается в 0o, то кривая y=sin(A-60o) начинается в 60o (т.е. ее нулевое значение на 60o правее ). Таким образом, говорят, что y=sin(A-60o) запаздывает относительно y=sinA на 60o. Составив таблицу значений, можно построить график функции y=sin(A-60o), показанный на рис. слева. Если кривая y=sinA начинается в 0o, то кривая y=sin(A-60o) начинается в 60o (т.е. ее нулевое значение на 60o правее ). Таким образом, говорят, что y=sin(A-60o) запаздывает относительно y=sinA на 60o.
График. y=sin(A-60o) (синусоида).
.gif) Составив таблицу значений, можно построить график функции y=cos(A+45o), показанный на рис. ниже. Составив таблицу значений, можно построить график функции y=cos(A+45o), показанный на рис. ниже.
Если кривая y=cosA начинается в 0o, то кривая y=cos(A+45o) начинается на 45o левее (т.е. ее нулевая величина находится на 45o раньше ).
Таким образом, говорят, что график y=cos(A+45o) опережает график y=cosA на 45o.
График. y=cos(A+45o) (косинусоида).
В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α.
Косинусоида имеет ту же форму, что и синусоида, но начинается на 90o левее, т.е. опережает ее на 90o. Следовательно, cosA=sin(A+90o).
Пример 5.
Построить график y=5sin(A+30o) в диапазоне от А=0o до А=360o
.gif)
Решение:
Амплитуда = 5, период = 360o/1 = 360o.
5sin(A+30o) опережает 5sinA на 30o т.е. начинается на 30o раньше.
График y=5sin(A+30o) (синусоида).
Пример 6.
Построить график y=7sin(2A-π/3) в диапазоне от А=0o до А=360o. 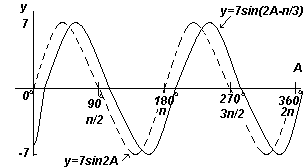
Решение:
Амплитуда = 7, период =2π/2= π радиан
В общем случае y=sin(pt-α) запаздывает относительно y=sinpt на α/p, следовательно 7sin(2A-π/3) запаздывает относительно 7sin2A на ( π/3)/2, т.е. на π/6 радиан или на 30o
График. y=7sin2A и y=7sin(2A-п/3) (синусоиды).
Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.
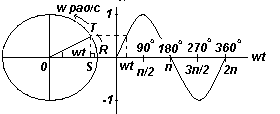
Пусть OR на рис. слева представляет собой вектор, свободно вращающийся против часовой стрелки вокруг О со скоростью ω радиан/с. Вращающийся вектор называется фазовым вектором. Через время t секунд OR повернется на угол ωt радиан (на рис. слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
Если все подобные вертикальные составляющие спроецировать на график зависимости у от ωt, получится синусоида с амплитудой OR.
График. Фазовый угол. Сдвиг по фазе.
Если фазовый вектор OR делает один оборот (т.е. 2π радиан) за Т секунд, то угловая скорость ω=2π/Т рад/с, откуда
Т=2π/ ω (с), где
Т - это период
Число полных периодов, проходящих за 1 секунду, называется частотой f.
Частота = (количество периодов)/(секунда) = 1/ T = ω/2π Гц, т.е. f= ω/2π Гц
Следовательно, угловая скорость
ω=2πf рад/с.
Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то
А - амплитуда
ω - угловая скорость
2π/ ω - период Т, с
ω/2π - частота f, Гц
α - угол опережения или запаздывания (относительно y=Аsinωt ) в радианах, он называется также фазовым углом.
Пример 7.
Переменный ток задается как i=20sin(90πt+0,26) ампер. Определить амплитуду, период, частоту и фазовый угол (в градусах)
Решение:
i=20sin(90πt+0,26)А, следовательно,
амплитуда равна 20 А
угловая скорость ω=90π, следовательно,
период Т = 2π/ ω = 2π/ 90π = 0,022 с = 22мс
частота f = 1/Т = 1/0,022 = 45,46 Гц
фазовый угол α = 0,26 рад. = (0,26*180/π)o = 14,9o.
Пример 8.
Колебательный механизм имеет максимальное смещение 3 м и частоту 55 Гц. Во время t=0 смещение составляет 100см. Выразить смещение в общем виде Аsin(ωt± α).
Решение
Амплитуда = максимальное смещение = 3м
Угловая скорость ω=2πf = 2π(55) = 110 πрад./с
Следовательно, смещение 3sin(110πt + α) м.
При t=0 смещение = 100см=1м.
Следовательно, 1= 3sin(0 + α), т.е. sinα=1/3=0,33
Следовательно α=arcsin0,33=19o
Итак, смещение равно 3sin(110 πt + 0,33).
Пример 9.
Значение мгновенного напржения в схеме переменного тока в любые t секунд задается в виде v=350sin(40πt-0,542)В. Найти:
а) Амплитуду, период, частоту и фазовый угол (в градусах)
б) значение напряжения при t =0
в) значение напряжения при t =10 мс
г) время, за которое напряжение впервые достигнет значения 200 В. 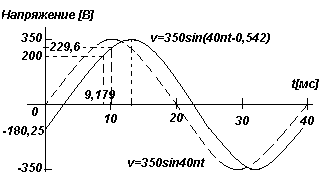
Решение:
а) Амплитуда равна 350 В, угловая скорость равна ω=40π
Следовательно,
период Т=2π/ ω=2π/40π=0,05 с =50мс
частота f=1/Т=1/0,05=20 Гц
фазовый угол = 0,542 рад (0,542*180/π) = 31oс запаздыванием относительно v=350sin(40πt)
б) Если t =0, то v=350sin(0-0,542)=350sin(-31o)=-180,25 В
в) Если t =10 мс, то v=350sin(40π10/103-0,542)=350sin(0,714)=350sin41o =229,6 В
г) Если v=200 И, то 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)
График. Колебательный механизм (пример, синусоида).
v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35o или 0,611 рад.
40πt= 0,611+0,542=1,153.
Следовательно, если v=200В, то время t=1,153/40π=9,179 мс
|

 главная страница / / Техническая информация / / Математический справочник / / Функции. Графики. Построение графиков. Чтение графиков. / / Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида.
главная страница / / Техническая информация / / Математический справочник / / Функции. Графики. Построение графиков. Чтение графиков. / / Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида.
 главная страница / / Техническая информация / / Математический справочник / / Функции. Графики. Построение графиков. Чтение графиков. / / Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида.
главная страница / / Техническая информация / / Математический справочник / / Функции. Графики. Построение графиков. Чтение графиков. / / Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида.

