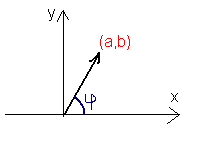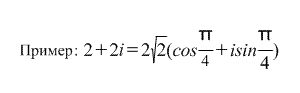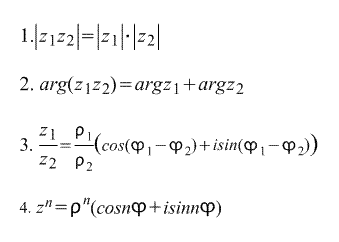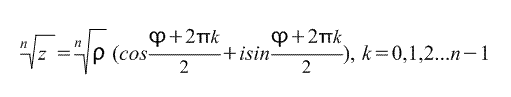Комплексные числа. Сложение, вычитание, умножение, деление комплексных чисел. Формулы. Тригонометрическая форма представления, формула Муавра и корень n-ной степени из комплексного числа.
Комплексные числа - это минимальное расширение множества привычных нам действительных чисел. Их принципиальное отличие в том, что появляется элемент, который в квадрате дает -1, т.е. i, или мнимая единица.
i 2= - 1
Любое комплексное число состоит из двух частей: вещественной и мнимой:

Таким образом видно, что множество действительных чисел совпадает с множеством комплексных чисел с нулевой мнимой частью.
Самая популярная модель множества комплексных чисел - это обычная плоскость. Первая координата каждой точки будет её вещественной частью, а вторая -мнимой. Тогда в роли самих комплексных чисел бдут выступать вектора с началом в точке (0,0).
Операции над комплексными числами.
На самом деле, если брать в расчет модель множества комплексных чисел, интуитивно понятно, что сложение (вычитание) и умножение двух комплексных числе производятся так же как соответственные операции над векторами. Причем имеется в виду векторное произведение векторов, потому что результатом этой операции является опять же вектор.
1.1 Сложение.
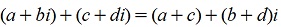
(Как видно, данная операции в точности соответствует покоординатному сложению векторов)
1.2 Вычитание, аналогично, производится по следующему правилу:
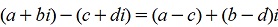 . .
2. Умножение.
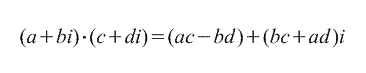
(см. векторное произведение векторов)
3. Деление.
Определяется просто как обратная операция к умножению.
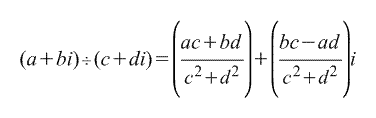
Тригонометрическая форма.
Модулем комплексного числа z называется следующая величина:
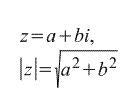 , ,
очевидно, что это, опять же, просто модуль (длина) вектора {a,b}.
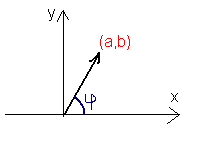
Чаще всего модуль комплексного числа обозначается как ρ.
Если представлять каждое комплексное число a+bi как вектор началом в точке (0,0) и концом в точке (a,b), то можно ввести еще одно понятие - угол, который этот вектор образует с положительным направлением оси х, то есть "правый" угол, который получается с осью х. (см. рисунок справа).
Величина этого ула в радианах называется аргументом комплексного числа и обозначается : arg z.
Оказывается, что
z = ρ(cosφ+isinφ) .
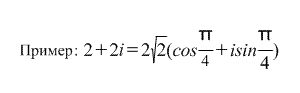
Непосредственно из тригонометрической формы записи комплексного числа вытекают следующие формулы:
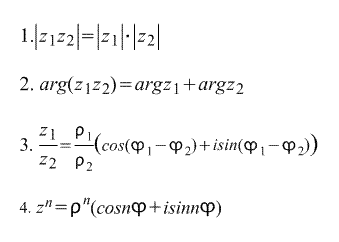
Последнюю формулу называют Формулой Муавра. Непосредственно из нее выводится формула корня n-ной степени из комплексного числа:
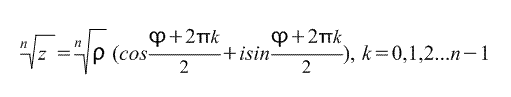
таким образом, существует n корней n-ной степени из комплексного числа z.
|
 главная страница / / Математический справочник / / Комплексные числа. Мнимая единица. / / Комплексные числа. Сложение, вычитание, умножение, деление комплексных чисел. Тригонометрическая форма представления, формула Муавра и корень n-ной степени из комплексного числа
главная страница / / Математический справочник / / Комплексные числа. Мнимая единица. / / Комплексные числа. Сложение, вычитание, умножение, деление комплексных чисел. Тригонометрическая форма представления, формула Муавра и корень n-ной степени из комплексного числа


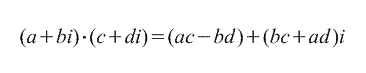
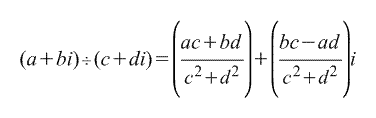
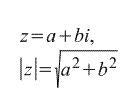 ,
,